Taro is here!

解説動画：
【これは流行る】新しいジャンケンを考えた！(ニコニコ動画)
【これは流行る】新しいジャンケンを考えた！(YouTube)

この記事の続き

これまでのじゃんけんは、手の種類が3つしかなかったので、
大人数でやると「あいこ」ばかりでなかなか勝負が決まりませんでした。
でももう、「あいこ」に悩まされることはありません！
手の数が 3, 5, 7, 11, ・・・, 31, ∞ のじゃんけんを実装したので、みなさんどうぞお使いください。
※「∞」は、正確には無限ではなく、手の種類の数は 2,000,000,000,003 通りですが、
1万人でじゃんけんしてもあいこになる確率は1％にも満たないため、安心してご利用下さい。

ジャンケンの手の種類の数35711131719232931∞

■使い方
1. 手の種類の数を選びます
2. 各プレイヤーの手を選択します
テキストボックスを選択後、円の中から好きな色を選んでください。
プレイヤーは何人でも追加することができます
3. 「勝敗を判定する」ボタンをクリックしてください
拡張されたじゃんけんのルールに従い勝敗を判定します

■解説
pを3以上の素数とします。
手の種類の数がp通りのじゃんけんのルールを考えます。

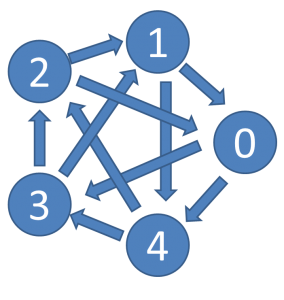
まずは5種類の手がある場合です。

この図のように、2人のプレイヤーで行うじゃんけんは、
1は0に勝つ
2は0に勝つ
2は1に勝つ
・・・
と、勝敗を定義します。

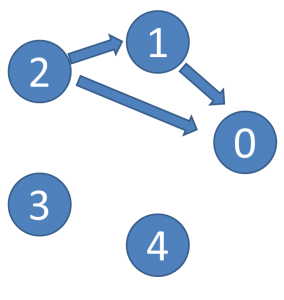
次に、プレイヤーが3人の場合ですが、
まずは以下の図のように隣り合う手 0,1,2 を選んだ場合を考えます。

この場合は、1対1の勝負で、
・2が1に勝つ
・1が0に勝つ
・2は0にも勝つ
ことから、
2→1→0
の順位とします。
これは自然な拡張と言えるでしょう。

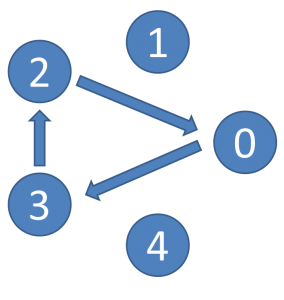
さて、問題は、3人の手が以下のような場合です。

1対1の勝負では、
・2は0に勝つ
・0は3に勝つ
・3は2に勝つ
ことから、
単純に考えると「あいこ」です。

しかし、「あいこ」としてしまってはつまらないので、できるだけ自然な拡張で勝敗を決めてやりたいと思います。

もう一度この図を見てみます。

1は0に勝っていますが、
2は0に勝っているだけではなく、1にも勝っています。

そこで、2つの手の勝負に対して、勝ち負けだけではなく「勝ち点」を考えたいと思います。

1 vs 0 : 1 に勝ち点 +1, 0に勝ち点 -1
2 vs 0 : 2 に勝ち点 +2, 0に勝ち点 -2

このように、隣り合う手については、±1の勝ち点、
1つ間を空けた手については、±2の勝ち点と定義します。

3手の勝敗について、
「リーグ戦をやって勝ち点を足し算する」
という形で、最終的なスコアを決めることにします。

そうすると、先ほどの0, 2, 3 の3手のスコアはそれぞれ次のようになります。

2 vs 0 : 2 に勝ち点 +2, 0に勝ち点 -2
3 vs 2 : 3 に勝ち点 +1, 2に勝ち点 -1
3 vs 0 : 3 に勝ち点 -2, 0に勝ち点 +2

0の勝ち点合計：0
2の勝ち点合計：1
3の勝ち点合計：-1

そこで、
2→0→3
を勝敗の順序とします。

これで、5種類の手があるじゃんけんで3種類の手が出た場合の勝敗が決まりましたね！
3人でじゃんけんする場合、普通のじゃんけんだと、少なくとも2回はじゃんけんをしないと1位から3位までが決まりませんが、
5手じゃんけんなら、最短で1回のじゃんけんで順位が決まります。

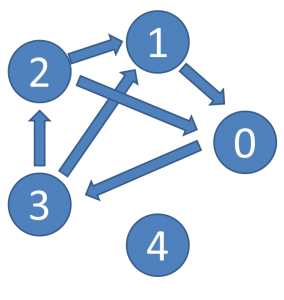
さて、
5種類の手があるじゃんけんで4種類の手が出た場合の勝敗も、
先ほどと同様に「勝ち点の合計」で決められるか、
見てみましょう。

1 vs 0 : 1 に勝ち点 +1, 0に勝ち点 -1
2 vs 0 : 2 に勝ち点 +2, 0に勝ち点 -2
3 vs 0 : 3 に勝ち点 -2, 0に勝ち点 +2
2 vs 1 : 2 に勝ち点 +1, 1に勝ち点 -1
3 vs 1 : 3 に勝ち点 +2, 1に勝ち点 -2
3 vs 2 : 3 に勝ち点 +1, 2に勝ち点 -1

0の勝ち点合計：-1
1の勝ち点合計：-2
2の勝ち点合計：2
3の勝ち点合計：1

というわけで、
2→3→0→1
の順番となりました。

5種類の手があるじゃんけん、これは使えそうですね！
「全員が同じ手」
もしくは、
「全種類の手が出る」
場合にしかあいこにならないため、
特に大人数でじゃんけんするときに威力を発揮します。

え？
「5種類の手のじゃんけんなんて勝敗ルールを覚えられない！！いちいち毎回計算してられない！！」
ですって？
そんなあなたのために用意したのが、冒頭の判定プログラムです。
どうぞご利用ください。

さて、
手の種類が5個のじゃんけんは、
「勝ち点の合計」
で順位が決められましたが、これは手の種類が5通りの場合だけなのでしょうか？

実は、
3以上の素数pに対して、
その中からq個（1<q<p とする）の手が出た場合に、
それぞれの勝ち点を合計すると、
全てのスコアが異なる値になることが、数学的に証明できます。（証明は後述）

つまり、
p種類の手があるじゃんけんでは、
この拡張ルールにより、
「全員が同じ手」
もしくは
「p種類全ての手が出る」
場合を除いて、
順位が決まることになるのです。

pとして十分大きな値を取れば、
何人でじゃんけんしようともあいこになることがほとんどなくなります。

それどころか、
単位円周上の点を適切に選べば、
無限個の手からなるじゃんけんも理論的には定義できます。

無限個の手からなるじゃんけんは、
コンピュータで再現するのは難しいため、
それに代わるものとして、
素数 2,000,000,000,003 を用いたじゃんけんを、
実行できるようにしました。
これなら、1万人で同時にじゃんけんしても、
あいこになる確率は 1% にも満たないので、安心ですね。
ここで言っている「あいこになる確率」というのは、
「誰か2人が同じ数字を選んでしまう確率」
のことです。
優勝が決まるだけでなく、
ほぼ間違いなく最下位までの順位が全て1回で決まるということです。

このじゃんけんについて特筆すべきは、
pがいくつであっても、
全ての手が、お互いに対等であるということです。
戦略についての小細工はいりません。
ただただ己の運を信じるのみです。

もちろん、コンピュータを使えば、
100人いようと1000人いようと、
全員のIDを「ランダムに1列に並べる」のは簡単です。
しかし、そうやって決められた順位にあなたは「納得」できますか？
本当に「ランダムに」並べられたのだろうか？という疑問は尽きません。
「勝つために何が必要だったのか」と考えても答えはありません。
じゃんけんなら、
全員が何の手を出したか公開した上で、誰の目にも検証可能な形で勝敗を決められます。

じゃんけんをトーナメント形式でやるのも、
そもそもその対戦相手の決め方に恣意性はないのか、という話になりますよね。
後出しできないようにする仕組みさえ整えれば、このやり方で全員が公平な立場で勝負できるというわけです。

というわけで、
今回は、一つの画面内で全員の手を入力する形のものを作ったわけですが、
これをアプリにして、参加者がスマホで一斉に手を選べるようにしたら、
みんな使ってくれないですかねえ。
何かのイベントで、参加者全員で一斉にじゃんけんとかしたら面白いような気もするんですけど。

■p手じゃんけんで、p-1個以下の手が出たときに、順位が決まることの証明
pを3以上の素数、
qを2以上p-1以下の整数とする。

p種類の手のうち、 を選んだとする。
で、X vs Y でXが得る勝ち点を表すとする。
このとき、X, Y を、 の中から任意に選んだ2つの点として、

となることを示す。

この式の、（左辺）－（右辺）を計算する。

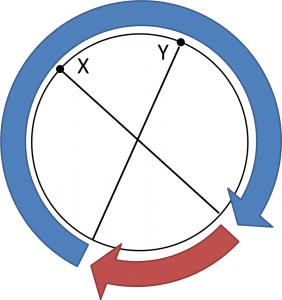
pが5のときと同様に、p種類の手を円周状に並べて考えると、 が下図の青い矢印で示した範囲にあるとき、

となり、赤い矢印で示した範囲にあるとき、

となる。

従って、赤い矢印で示した範囲にある点の数をdとして、

となる。

pが素数であることと、q と s(X, Y) がともにpより小さいことから、この値は0にはなり得ない。
（証明終わり）

→続き