こちらのゲームについての説明です。
変形のルールについて
青いテーブルのセルをクリックすると数字が変化しますが、そのルールは以下の通りです。
- テーブル内の数字は、0から4までの整数値のみを取る。足し算や掛け算は、通常の整数としての足し算や掛け算の結果を5で割った余りとして定義する
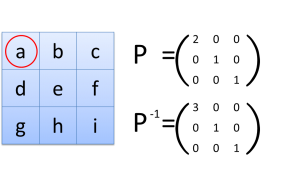
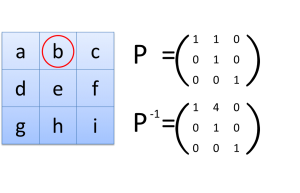
- i行j列をクリックしたとき、行列Pを、3×3の単位行列のi行j列に1を足した行列とする
- テーブルを3×3の行列だと思って、左からPを、右からPの逆行列をかける
「位数5の有限体上の正方行列に対する相似変換を行っている」と言うことができます。
これを繰り返して対角行列、もしくは、ジョルダン標準形へ変形するのがゴールです。
変形の例
左上のセルをクリックしたときのPとPの逆行列はこのようになります。
Matrix Example 1
真ん中の上のセルをクリックしたときのPとPの逆行列はこのようになります。
Matrix Example 2
線型代数がパズルになった！！
Level 1, Level 2, Level 3 は、Goal の行列の形が違っています。
Level 1 の行列は、どこをどうクリックして変形させても、Level 2 のGoal の行列になることはありません。
このあたりの話が、理系の大学生にはおなじみの、線型代数のジョルダン標準形の話になるわけですね。
ちなみに、このゲームでは、初期値の選び方によってはジョルダン標準形に変形できないものもあります。
固有方程式が因数分解できない場合はだめです。
何となく、ジョルダン標準形に変形すること自体がパズルみたいなものではないかと思い、できるだけ簡単な操作でこれを実現することを考えました。
その際、
「分数の計算なんてしたくないよね」
と考えたため、有理数ではなく、有限体上の行列にしました。
最近では、高校でも行列を扱わなくなったりしているようですが、このゲームなら、クリックするだけでなんとなく変形されるので、小学生でもできちゃいます。
「最近の日本の小学生は、行列の対角化ができるらしいぜ」
「まじかよ！小学生で？Cool Japan パネェな」
みたいな会話が海外で繰り広げられると思うと興奮を禁じ得ません！！これは流行らせたい。
と、言ってみたものの
「流行るわけねーだろwww」と言う声が聞こえるようです。
これ、やってみるとわかるのですが、クリックしたときの数字の変化の仕方が、全く直感的じゃないんですよね。
適当にクリックしていると、段々と「ああ、この辺の値が変わるのかな」というのが何となく掴めて来て、そのうち何となくクリアできるのですが、クソゲー感が満載ですね。
万人受けする気が全くしないので、少しでも興味を持つ人に届くように、一応英語でも説明を書いておきます。