Taro is here!

高校数学で複素数を習った際、
「何これ？何の意味があるの？」
という疑問を持った人は多いのではないでしょうか。

それまでは、
「2次方程式は、解を持つ場合と持たない場合がある」
という話だったのに、それを無理矢理
「2乗すると-1になる数を考えて解いてみましょう」
と言って計算させて、何なのこれは？という話です。

確かに、
「虚数単位『i』は、普通の文字だと思って計算し、ただし、2乗すると-1になる」
という計算ルールに従って計算すれば、式変形はできるのですが、
なぜそんな計算をする必要があるのでしょうか？

そこで、
「数の概念を拡張してまで解きたい二次方程式」
として、数列の三項間漸化式を考えてみたいと思います。

複素数というものを新たに導入する動機づけがほしい

「何の役に立つのか？」
を簡単に説明する事例を挙げるのは、結構難しいです。

三次方程式の解の公式（カルダノの公式）で必要になることを説明するのが、本当はいいのでしょうが、これは結構難しい内容になります。
「交流回路の計算で使われる」という話が紹介されることはありますが、具体的に計算式を示すには、まず電気についての説明が必要になります。

高校数学の範囲で、もっと単純に以下のような例はないでしょうか？

• この2次方程式は実数解を持たない。でも、「解なし」じゃ困る。どうしても解がほしい

こういう例が一つあれば、
「ああ、そういうときに役に立つのね。そういうことは他にもありそうだね」
と、納得できる気がします。

ただ、そういう例はなかなか出てきません。

というのも、2次方程式が出てくるのは、例えばこういう場合だからです。

長さ16cmの紐があります。
この紐を使って、面積が15平方センチメートルの長方形を作るには、1辺の長さをいくつにすればよいでしょう？

一辺の長さをxとすると、こういう式になります。

変形します。

これを解くと、こうなります。

3cm×5cm の長方形を作ればいいということになりますね。

では、問題がこうなるとどうでしょう？

長さ16cmの紐があります。
この紐を使って、面積が17平方センチメートルの長方形を作るには、1辺の長さをいくつにすればよいでしょう？

同じく一辺の長さをxとして方程式を作ります。

変形します。

これは実数解を持ちません。
無理矢理解くと

となりますが、こうやって無理矢理解いた答えに意味はあるでしょうか？
ありませんね。

「面積17平方センチメートルにはできない」
というのが答えになります。

こんな風に、高校の数学の「複素数」以外の単元で出てくる2次方程式は、
実数解がなかったら「実数解がない」こと自体に意味があるのであって、
「それでも無理矢理解きたい」
と思うケースがほとんどないのです。

そんな中、「解なし」では困る、と辛うじて言えそうだなと個人的に思ったのが、
数列の三項間漸化式でした。

数列の三項間漸化式とは

数列の三項間漸化式は、こういうものです。

こちらの一般項をnの式で表す問題です。

これ自体、高校の学習指導要領には入っておらず、「発展的な内容」として紹介されるに留まるもので、微妙と言えば微妙なのですが、私が高校生の時は以下の解き方を教わりました。

まず、左辺に集めます。

これの係数をそのまま二次方程式の係数にした、「特性方程式」を作ります。

解きます。

解と係数の関係から、以下が言えます。

これを使うと元の漸化式がこうなります。

この式は、以下の2通りに変形できます。

まず最初の式を元に、
添え字を順番に減らして行くと以下が得られます。

同様に、2番目の式より以下が得られます。

ここに、

を入れます。

上の式から下の式を引くと、

となり、n番目の数をnの式で表すことができました。

この問題は、漸化式の係数が変わっても、
「特性方程式」なる2次方程式が、2つの異なる解を持つ限り、
全く同じ解き方で解くことができます。
重解の場合はちょっと工夫が必要です。

では、特性方程式が実数解を持たない場合はどうでしょうか？
「n番目の数をnの式で表すことはできない」
が答えになるのでしょうか？
それはちょっと悲しいですね。

でも、虚数解を許せば、全く同じように一般項をnの式で表すことができるのです。

「三項間漸化式は、特性方程式の解が虚数の場合も、同じように計算して一般項をnの式で表すことができる」
ということ自体は、三項間漸化式の解き方の紹介の際に、さらりと触れられることはあります。

ただ、ここはさらりと触れて終わりにするべきところではなく、むしろ、

• この2次方程式は実数解を持たない。でも、「解なし」じゃ困る。どうしても解がほしい

という、複素数の範囲まで数の概念を拡張したい積極的な理由になる、高校数学の範囲の中の数少ない例の一つだと思うのです。

虚数解を使って無理矢理解くことに意味があるのか？

これで納得できればいいのですが、

• わかったけど、そんなに無理してまでn番目の数をnの式で表して、何かいいことはあるのか？

という疑問を持つかもしれません。

これはもっともな疑問で、実際、

をnの式で表すと、

となるのですが、じゃあ

を計算するために

を2項展開するのか？というと、却って面倒です。
n=3,4,5,…
と、10番目まで順番に求めたほうがいいでしょう。

つまり、何も便利になっていない！

というわけで、確かにこのままでは、
「ほら、複素数って便利でしょ？」
とはならないのです。

もう一歩踏み込んでみましょう。

数列の性質が分かる

三項間漸化式は、特性方程式が異なる2つの解αとβを持つ場合、先ほどの例のように計算することで、一般項を以下のように表せます。

pとqは、初期条件によって定まります。

このように、n番目の項をnの式で表すメリットの一つは、数列の大まかな特徴がわかることです。

例えば、

• αとβが実数で、どちらも絶対値が1より小さいときは、nが大きくなると、a_nは0に収束する
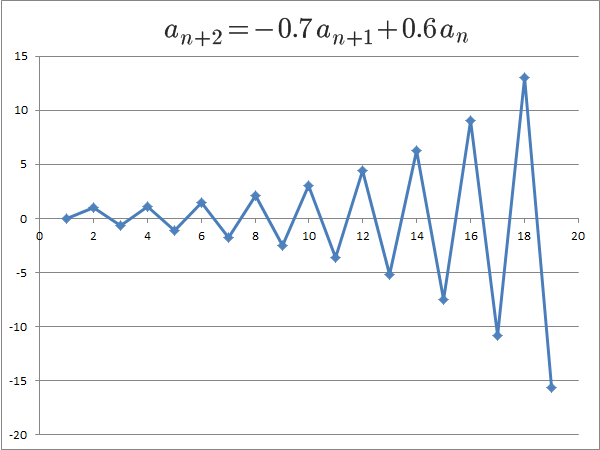
• αとβが実数で、どちらかの絶対値が1より大きいときは、nが大きくなるとa_nの絶対値が指数関数的に大きくなる

a_nをnの式で表すことによって、
このような、数列の大局的な性質を知ることができます。

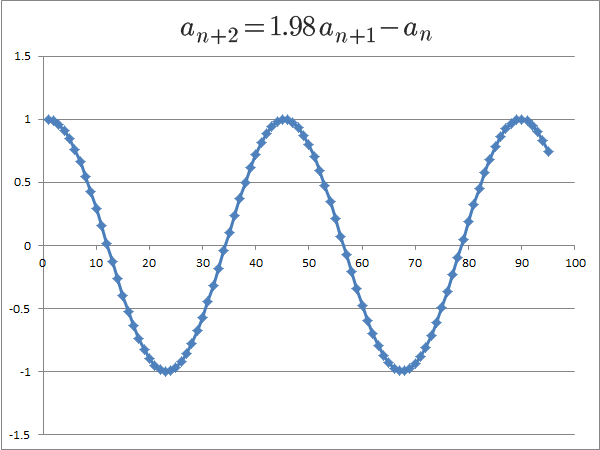
実際に、グラフにしてみましょう。

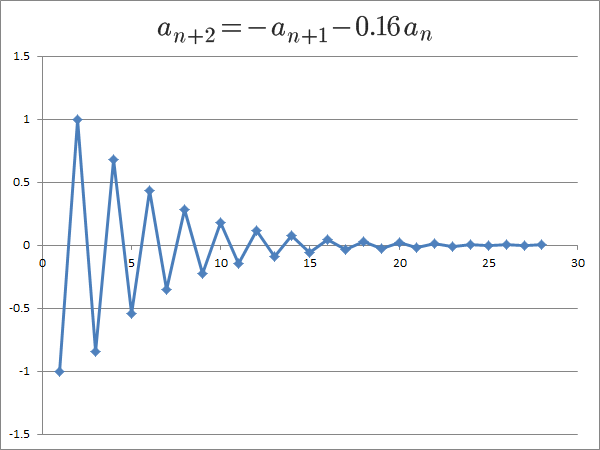
解が虚数の場合は、次のことが分かります。

• 解の絶対値が1より小さければ0に収束する
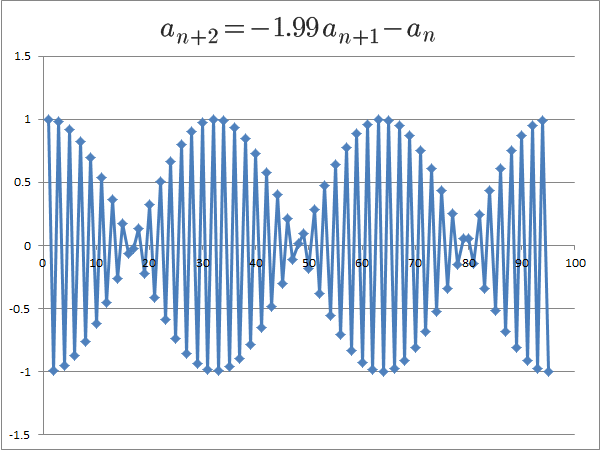
• 解の絶対値が1より大きいときは、nが大きくなるにつれて段々大きい値を取るようになるが、実数の場合と異なり、nが大きくなっても0付近の値を取ることがある

こちらもグラフにしてみましょう。

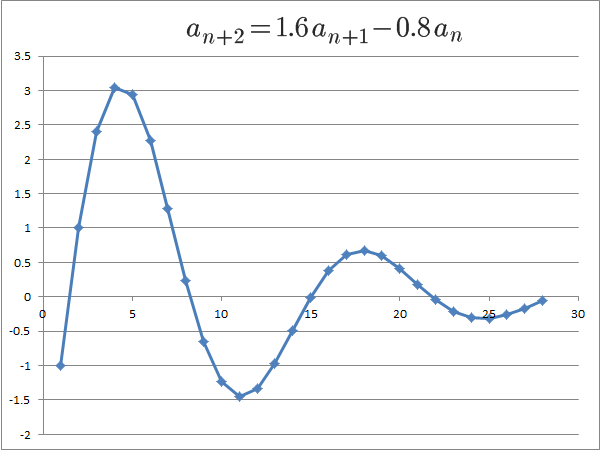
変わった挙動を示すのが、
解の絶対値が1に等しいときです。
複素数αの絶対値が1のとき、αを何乗しても、複素平面上の単位円の上をぐるぐる回るだけなので、収束も発散もせず、一定の範囲内の値を取ることがわかります。

これも具体的に見てみましょう。

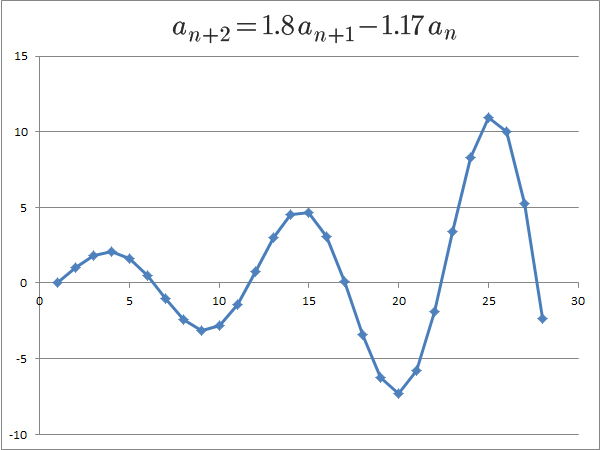
特性方程式が虚数解を持ち、かつその絶対値が1になるのは、このようなときです。

特に初期条件が、

のときをグラフ化してみます。

このように、三角関数のグラフのような形になります。

こうした性質は、複素数を使った一般項の表記を使えば容易に説明できることですが、
元の漸化式からはすぐにはわかりません。

という漸化式を使って、n=1,2,3,…と順番に計算していくと「三角関数が現れる」というのは、意外な結果ではないでしょうか。

係数が少し変わっただけで挙動が大きく変わるので、漸化式そのものを眺めているだけではこういったことはわからないのです。

まとめ

• この2次方程式は実数解を持たない。でも、「解なし」じゃ困る。どうしても解がほしい。
  という例はあるか？
  →ある。例えば、数列の三項間漸化式。
• そうまでして一般項をnの式で表すことに意味がある？
  →ある。そうすることで、数列の性質が説明できる。

 

複素数の意義を説明する一つの例としてどうでしょうか、という話です。

ところで、この説明に納得せず、
「そんなこと言うけれど、数列の挙動が三角関数みたいになるんだったら、そもそも複素数なんか使わなくても三角関数を使って一般項をnの式で表せるのでは？」
という高校生がいたら、それは相当見込みありますよね。
「では、実際にやってみよう」
で、次のステップに進むことができます。

ただ、
「そもそも、特性方程式が虚数になるような三項間漸化式が出てくるのはどういうときですか？」
と言われるとちょっとつらいです。
簡単な確率の計算で三項間漸化式が出てくることはあるのですが、
「特性方程式が虚数になる三項間漸化式が出てくる例題を作れ」
と言われると難しいです。
人によっては、ここまでないと、「役に立った」という感覚を持てないかもしれません。
どなたかいい例を知っていたら教えてください。