Taro is here!

今さら感があるのですが、今年の東大の数学の入試問題では、2015年にちなんでこんな問題が出たそうです。

いきなり2015で考えると難しいので、1,2,3,・・・と順番に考えていって、規則性を見つけるのがこういう問題のセオリーですが、さて、その規則とは？

問題の解答自体を解説しても面白くないので、その規則を可視化したものをご紹介します。

パスカルの三角形

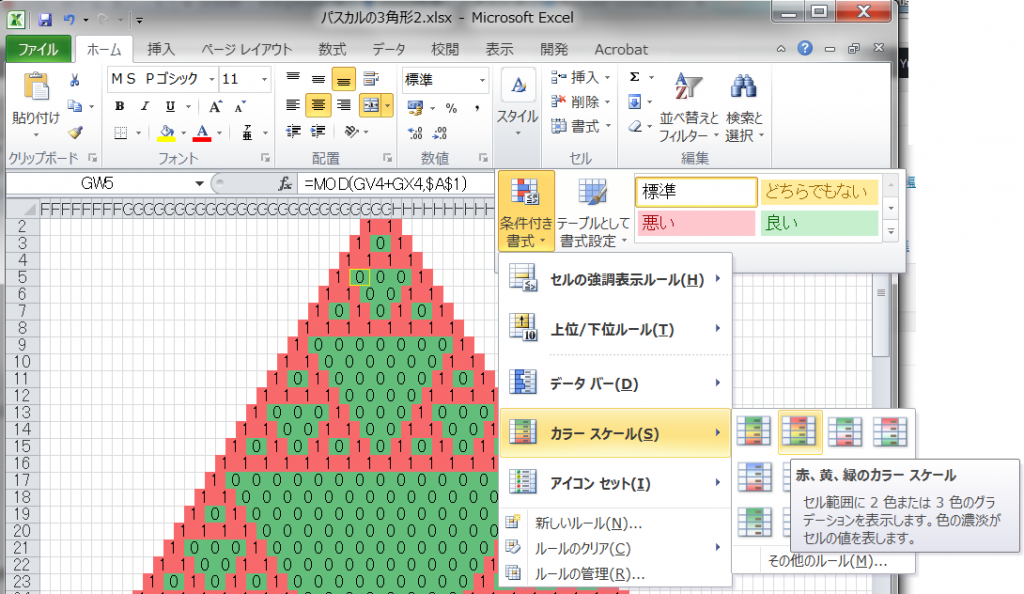
パスカルの三角形を、2で割った余りで色づけしてみます。
Excel方眼紙を使って、条件付き書式でいっぺんに色づけします。
プログラミング不要で簡単ですね！

ポイントは、パスカルの三角形を下まで書いた後で2で割るのではなく、1行ずつ2で割った余りを出して行けばよいことです。計算が簡単です。
試験中はExcelなんて使えませんが、手計算で10行目くらいまでは簡単に書けるでしょう。
そうすれば法則が見えてきます。

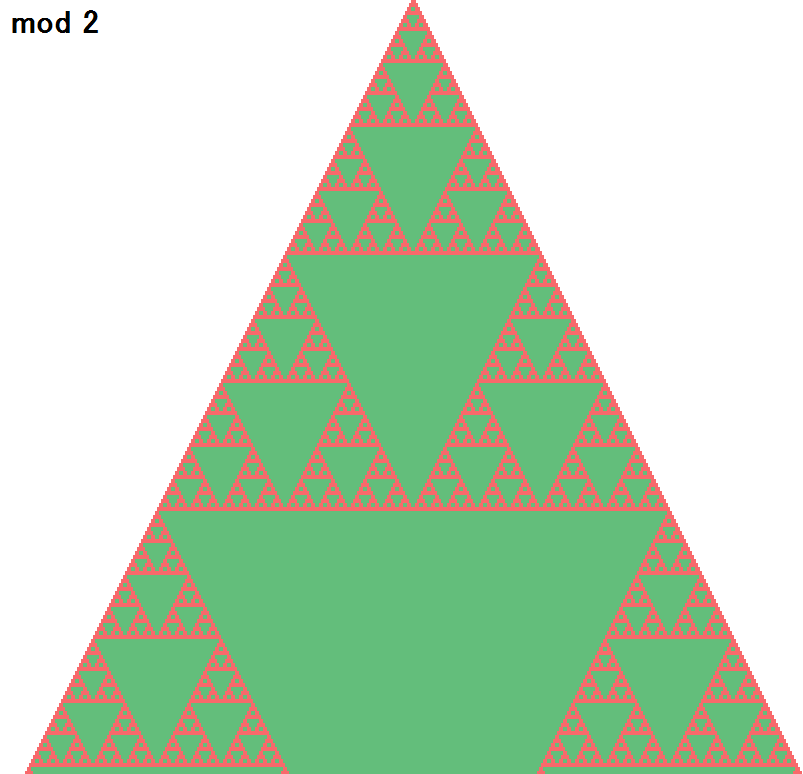
150行くらいを描画したのがこちらになります。

ご覧の通り、非常に規則的な形をしています。
小さい三角形が繰り返し現れ、小さい三角形のパターンを大きい三角形が同じように繰り返しています。

これを踏まえた上で、2015行目がどうなっているかを類推すれば、問題は解けるでしょう。

2ではなく、3,4,5,・・・の余りだとどうなるか？

ここからが本題です。

パスカルの三角形を、2で割った余りで色づけしたらこのような面白い模様になりましたが、
3,4,5,・・・の余りだと、どんな模様が現れるのでしょうか？

実際にやってみましょう。
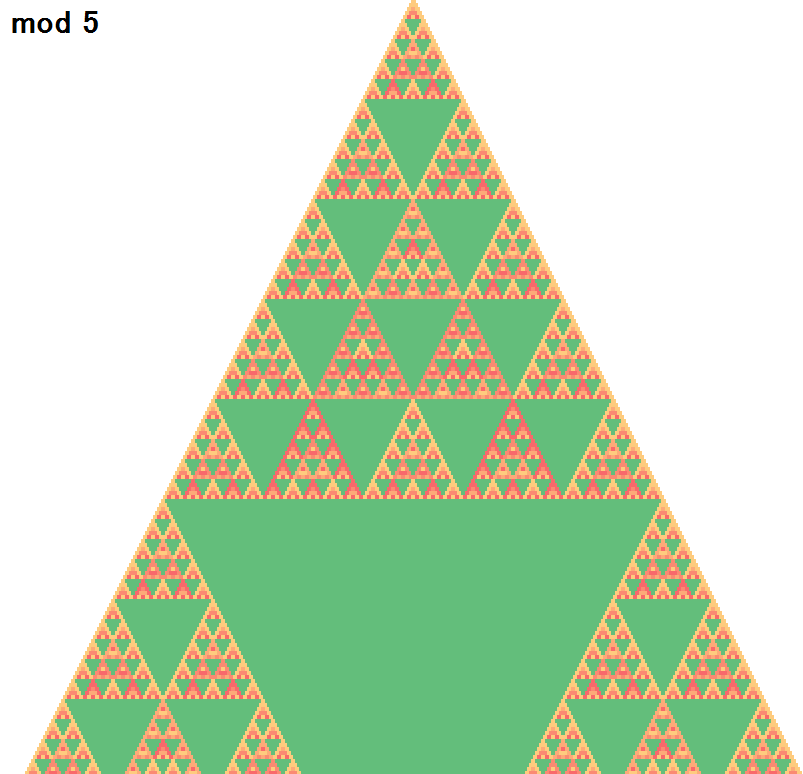
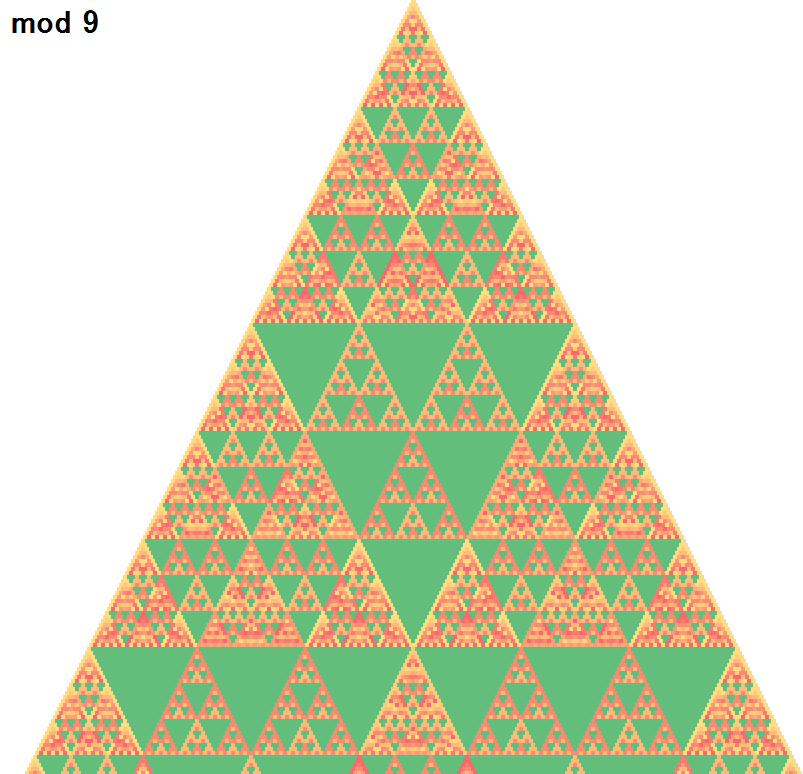
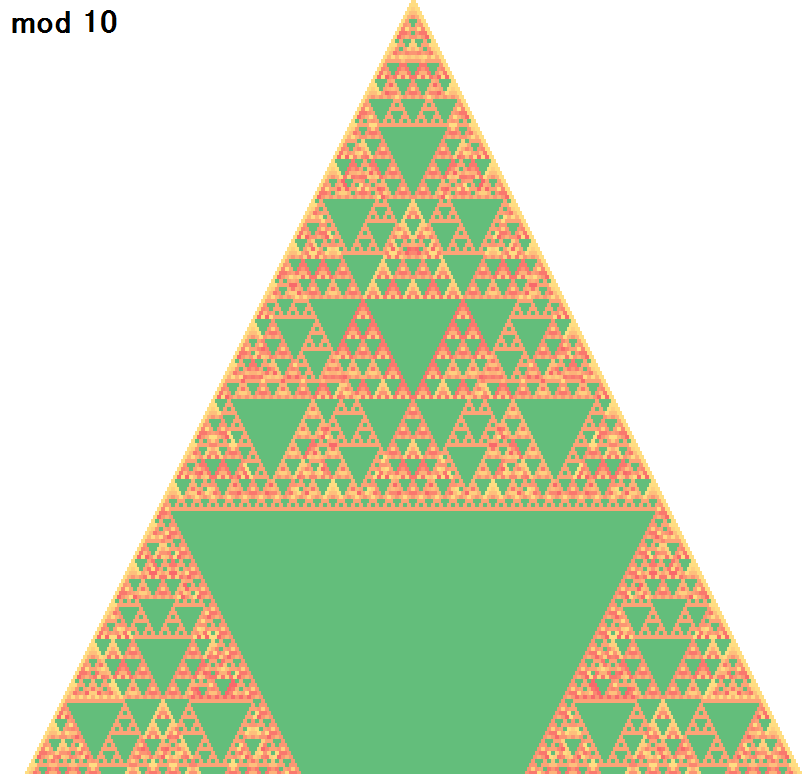
一気に3から16まで見ていきます。

面白い形ができましたね！

何とも不思議な形ですが、よく見比べると以下の特徴が見えてきます。

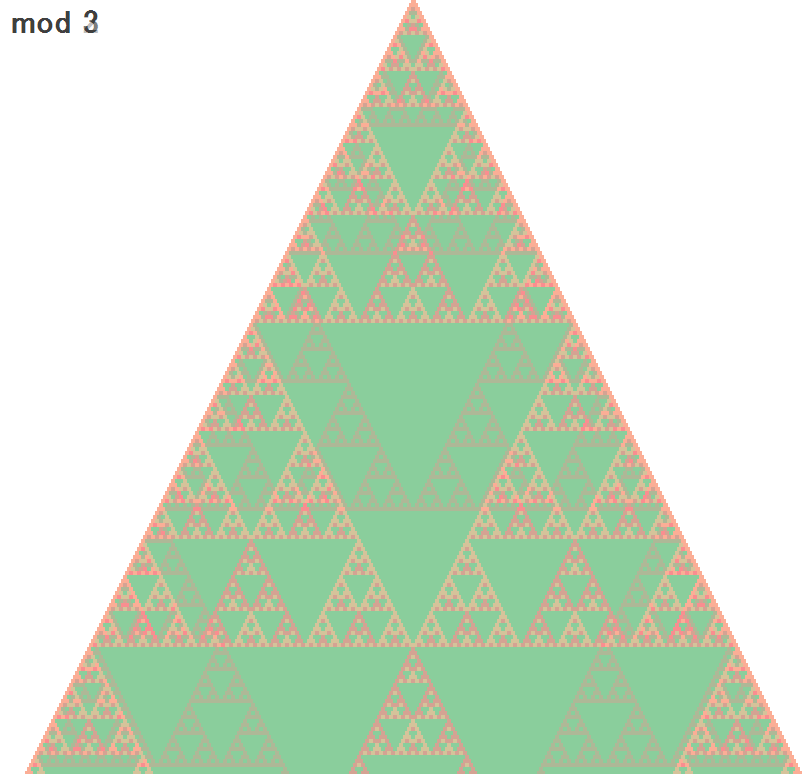
1. 素数のときは整った形になる
2. 素数のn乗のときも、ある程度整った形になる
3. 合成数の時は、複雑な形になる。特に、約数の模様を重ねたような形になる

3番目の補足です。
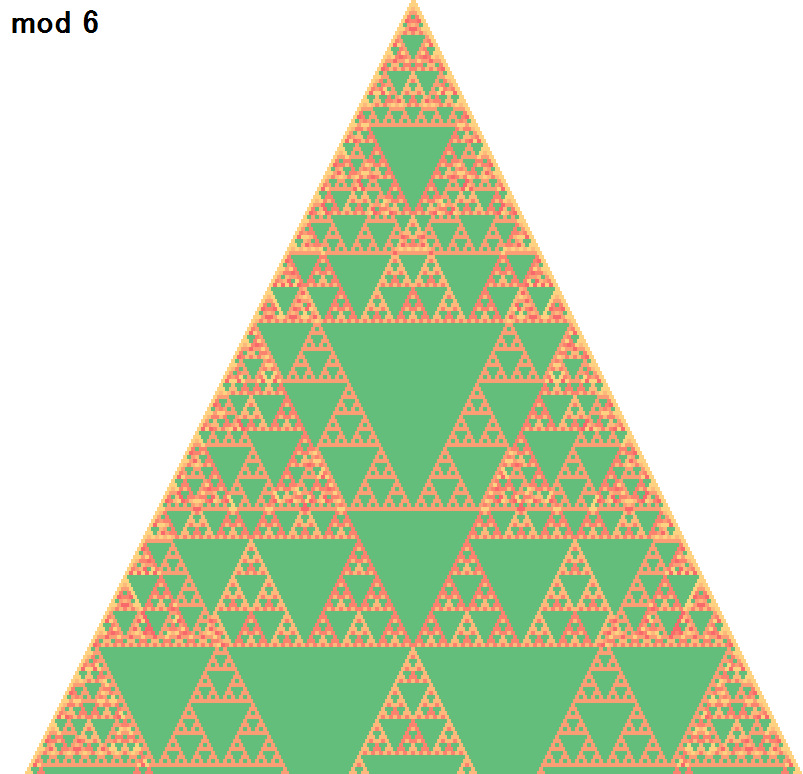
mod 2の三角形とmod 3の三角形を重ねたものが以下の図になりますが、mod 6の三角形とパターンが同じですよね。

mod 6の三角形（再掲）

6で割った余りを考えると、

• 2で割った余りが0、3で割った余りが0　→ 6で割った余りが0
• 2で割った余りが1、3で割った余りが1　→ 6で割った余りが1
• 2で割った余りが0、3で割った余りが2　→ 6で割った余りが2
• 2で割った余りが1、3で割った余りが0　→ 6で割った余りが3
• 2で割った余りが0、3で割った余りが1　→ 6で割った余りが4
• 2で割った余りが1、3で割った余りが2　→ 6で割った余りが5

というように、2で割った余りが何で3で割った余りが何か、で特徴づけられることから、このような重ねあわせたものが6で割った余りの模様になることが説明できます。

群論の言葉で言うと、

が成り立つことから、このような重ね合わせの仕組みが説明できます。
逆に言うと、ちょっと強引ですが、この法則を可視化したのがこの三角形模様とも言えるでしょう。

非可換群の場合だとどういう模様になる？

ここまでの話を踏まえると、次に湧いてくる疑問は、

非可換群の場合はどうなるのだろうか？

ですね。
上の2つから下の値が決まるので、本当は群である必要すらないのですが、広すぎてわからなくなるので、とりあえず群で考えましょう。

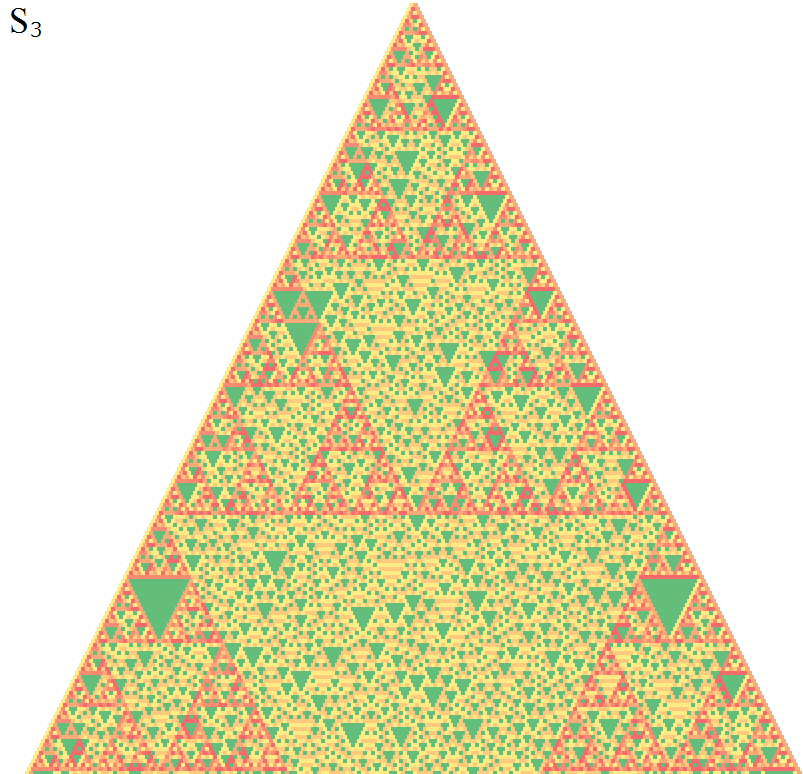
最も単純な非可換群である、3次対称群で描画してみたところ、このようになりました。

一番上の頂点を一つの値から始めると、巡回部分群が現れるだけになってしまうので、別のサイクルの元を2つ隣に並べたところから始めています。

mod n のパターンとは違う、複雑な図形になりました。
非可換群なので、左右非対称になっていますね。
穴ぼこだらけで、スポンジボブっぽい感じです。

特徴的なのは、赤とオレンジで、mod 2 のときの図形がうっすらと現れていることです。

これは、3次対称群  が3次交代群  を正規部分群に持ち、

となることから説明できます。

準同型写像  をパスカルの三角形の各元に適用する操作を考えると、
 でパスカルの三角形を作ってから適用するのと、
最初の1行に適用してから  のパスカルの三角形を作るのが、
同じ結果になることからわかります。

これを一般化すると、

ある群で作ったパスカルの三角形は、その商群で作ったパスカルの三角形のパターンを内部に持つ

と言えそうです。

では、正規部分群を持たない群だったら？

正規部分群を持たない群つまり、非可解群と言えば、5次の交代群がありますね。

それでは見ていただきましょう。
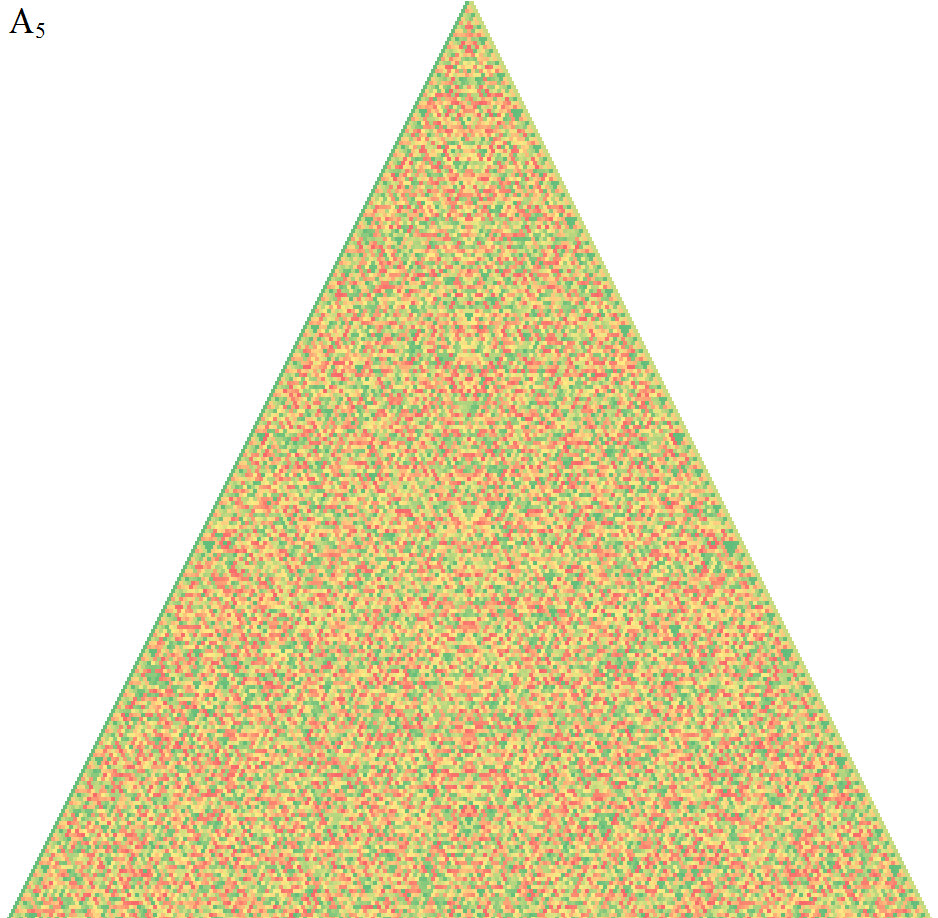
5次の交代群で作ったパスカルの三角形です。

いやー、複雑ですね。

これまでとは大きく違う、乱雑な並びです。

もう少し進んだら規則的な模様が現れるかと思って、三角形の下の方まで描画してみたのですが、それでもこんな感じでした。

これは複雑です。
この感じだと、これより複雑な群を作っても、見た目はあまり変わらないでしょうね。
非可解群、恐るべし。

ちょっとだけ考察

先ほどの3次対称群と違うのは、穴ぼこがあまりないことです。
ぎっしり詰まった感じです。

3次対称群のパスカルの三角形に多数現れている穴ぼこは、
単位元が集まってできた下向きの三角形ですが、
5次の交代群の場合には、このような穴ぼこはできないのでしょうか？

一応、これを考察すると、

任意の群で作ったパスカルの三角形には、いくらでも大きな「穴」がある

が証明できます。
なので、5次の交代群のパスカルの三角形にも、もっと下の方まで行けば、いくらでも大きな穴があるということになります。

また、5次の交代群のパスカルの三角形には、規則が全くないようですが、そうではなく、例えば以下のように左端4列だけを見てみれば、繰り返し同じ模様が現れていることが分かります。

左から5列、6列、・・・で見ても、繰り返し同じ模様が現れますが、その周期が指数関数的に長くなるので、見た目には周期的な模様には見えないのです。
そして、この周期に合わせるように、段々大きな穴ぼこが現れてきます。
左4列の図中には、緑色の小さい三角形（3ブロックから成るもの）が、周期の端に現れています。

簡単そうに見えて意外と難しかった

最初に紹介した東大の入試問題は、パッと見で

「なんか簡単そう～」

「無理矢理2015にちなんだ問題なんか作っちゃって～」

と思ってしまいましたが、奥にはこんな話が待っていたんですね。

このあたりの話を一般化した研究も、よく知りませんがきっとあるのでしょう。
難しそう～。