Taro is here!

前回の記事で、パスカルの三角形を色分けすると様々な不思議な模様が現れるのを見ました。
今回は、それを応用して平面を埋めつくすパターンを考えてみましょう。

前回のおさらい

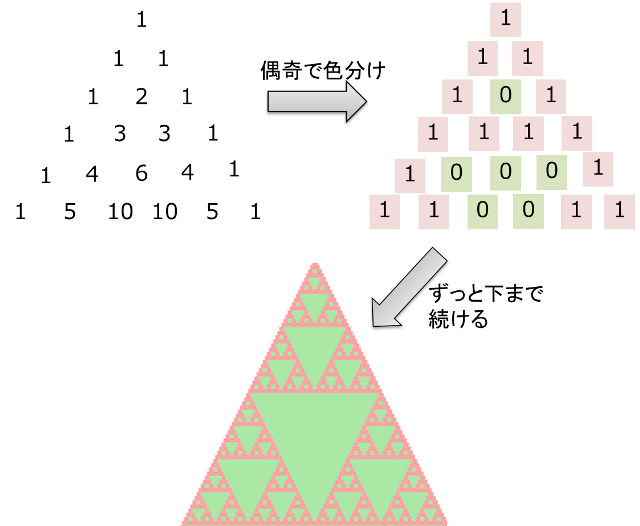
前回やっていたことは何かと言うと、パスカルの三角形を例えば2で割った余り、つまり偶数か奇数かで色分けしてみよう、というものです。

そうするとこのように、自己相似形のフラクタルっぽい模様が現れるわけです。
前回はこれをさらに、3色、4色、・・・で色分けしたときのパターンも確認しました。

最初の一行を、「1」から始める必要はない

ここでやっていることのポイントは、

1行目から2行目を計算、
2行目から3行目を計算、
・・・

という、「上の行から下の行が決まる」という仕組みです。
そうすると、1行目は何でも良いから決めさえすればよい、ということになりますね。

これまでは、

「・・・ 0 0 0 0 1 0 0 0 0 ・・・」

から始めていましたが、例えば、

「・・・ 0 1 1 0 1 1 0 1 1 ・・・」

という、3つずつの繰り返しの行から始めた場合、次の行も同じパターンになります。

このように、1行目を、左右共に無限遠まで続く、一定周期の繰り返しにした場合、縦方向も一定の間隔で周期が続くので、平面を埋めつくすパターンができます。
（最初の行に戻るとは限りません。途中で全部0になる場合もあります）

というわけで、このようにパスカルの三角形の応用で現れる模様をいくつか見てみましょう。

1行目のパターンによっては、左右非対称な模様になる場合もあります。
微妙に気持ち悪い模様もありますが、何かのデザインに使えないでしょうか？

横方向の繰返し周期を長くするとどんどんパターンは複雑になります。

次に、2色ではなく3色にしてみましょう。

このように、横方向の周期だけでなく、色の数も何色にでも増やすことができます。

以下は、7色の例です。

やり過ぎるとぐちゃぐちゃになります。

非可換群の場合

前回の記事と同様に、非可換群で同様のパターンを作ってみましょう。
以下は、5次交代群で作ったパターンの例です。

何とも言い難い模様ですが、開始行の周期、初期値と色を上手く選べば、面白い模様が作れるかもしれません。
気が向いたら色々試してみたいと思います。