Aさんは円形の池の真ん中でボートに乗っています。
岸には、Aさんを捕まえようと待ち構えている鬼がいます。
鬼はボートの4倍の速さで池の周りを走れます。
Aさんは鬼に捕まることなく上陸して逃げることはできるでしょうか?
という、問題があります。
ずいぶん昔に聞いたものなのですが、出所はどこだったのかと思ってググってみたら、
どうやら「ビル・ゲイツの面接試験」という本に載っている問題のようです。
Q&Aサイトで質問している人もいました。
さて、この問題の答え自体は、
聞けば「あー、なるほど」というパズル的なものなのですが、
では、
「鬼の速さがボートの何倍までだったら逃げ切れるのか?」
「池が円形ではなく別の形だったらどうなのか?」
と考えると、そんなに簡単ではありません。
とりあえず、
鬼の速さがボートの4.6倍くらいまでなら逃げ切れそうだということと、
池の形が正方形だった場合は5.7倍くらいまで大丈夫そうだ、
ということはわかったので、
それらについて書きたいと思います。
一般的な計算方法は、よくわかりません。
「凸な形状の池について考えた場合、池が円形のときに最も逃げづらい」
という気がするのですが、どう証明したらよいでしょうか?
難しそうです。
最初の問題の答え
まず、元の問題、
鬼の速さがボートの速さの4倍だったときに、
どうやったら捕まらずに上陸できるか?
についてです。
(答えを見たくない人のために下の方に書きます)
この問題、「3倍」だったら簡単なのですが、
「4倍」なのが難しいポイントです。
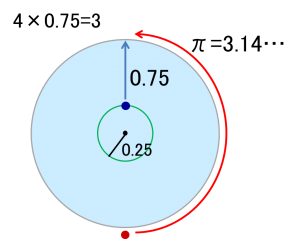
中心からまっすぐ岸に向かう場合、
鬼と正反対の方向に向かっても、池の半周が半径の3.14…倍なので、4倍の速さで走られると先回りされてしまいます。
それで、
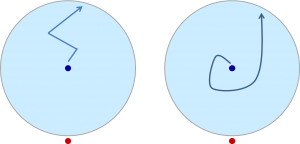
「うずを巻くように回転しながら進むのか?」
「ジグザグに進むのか?」
と考えてしまうと、
「曲線の長さを計算するなんて難しすぎる!」
となってはまってしまいます。
実際にはそんなに難しいことを考える必要はありません。
答えは、
池の中心の周りを、池の4分の1の半径より少しだけ小さい円を描きながらぐるぐる回って、
鬼との位置関係が池の中心を挟んで正反対になるようにする。
その後、鬼と正反対の方向にまっすぐ進んで岸に向かう
です。
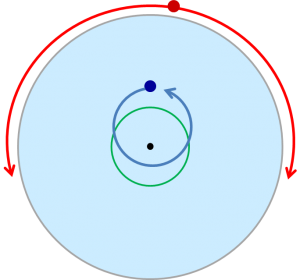
半径を1とした図だと思ってください。
緑色の円をボートが1周するのと、鬼が1周するのにかかる時間が同じです。
なので、これより内側を回っていれば、
いつかは鬼と中心を挟んだ反対側の位置に行くことができます。
そうなったタイミングで、鬼と反対方向に進めば、鬼に捕まらずに岸に上がれます。
この方法なら、鬼の速さが π+1=4.14… 倍までなら逃げ切ることができます。
鬼の速さがボートの何倍までだったら逃げ切れるか?
さて、ここからが本題です。
4.14倍よりもっと鬼が速くても逃げ切れるのかどうか、です。
問題を考えやすくするために、
ここからは池の半径を1、鬼の速さを1、ボートの速さをv(0<v<1)とします。
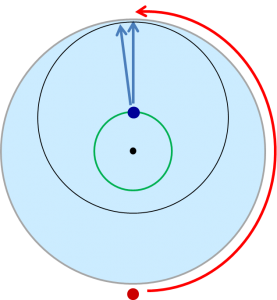
とりあえず、
半径vの円周の少し内側を回ることで、
ボートと鬼が円の中心を挟んだ反対側の位置に来るようにすることができます。
逆に、半径vの円より少しでも外側を移動する場合、
円の中心から見たときの角速度(1秒あたりどれくらい回転方向に移動できるか)が、
1より大きくなってしまうので、
鬼は必ず「正反対の位置」よりも近づいてしまいます。
なので、
ボートが半径vの円より外側にいて、かつ、鬼が「正反対の位置」にいる
という状態を作ることはできません。
別の言い方をすると、
そのような位置関係にならないように鬼は動くことができる
ということです。
例えば、
半径v以下の円で、中心が円の中心からずれているところをぐるぐる回ったらどうか?
と考えたとしてもこれはダメで、
こっちが一周する間に鬼も一緒になって一周してはくれず、
適度なところで折り返してきます。
また、これは、
半径vの円の一歩外に出れば、鬼はもう近づいて来る一方だということを意味しています。
つまり半径vの円の外側でどんな動きをしたとしても、
鬼はもはや方向転換をすることはなく、最初に動き出した方向に走り続けます。
とすれば、半径vの円の外側に出た瞬間からもう鬼を攪乱することはできないのだから、
岸のどこかに向かって最短距離で向かう以外にありません。
最短距離ということは直線です。
また、
先ほど述べた通り、半径vの円の外に出た瞬間から、
鬼は一方向に向かって回るのが「最も効率が良い」ので、
半径vの円周上で、鬼がどちらに向かって走り出すか見極めてからこちらが岸に向かって走り出せば、
鬼が切り返してくることはありません。
切り返してきた場合は、それは単純に鬼にとって不利な行動なので、
鬼がちょうど「正反対の位置」を超えたタイミングで、
改めて向かう岸辺の点を変えればOKです。
以上、まとめると、
最善の行動は、
中心からの距離がvの位置にボートがいて、
鬼が正反対の位置にいる状態にして、
鬼が時計回りか反時計回りのどちらに走り始めるか見極めてから、
円周上のどこかの点に向かって一直線に移動する
ということになります。
以下、鬼が反時計回りに走り始めたとして考えます。
「一直線に向かうべき先」は、「もっとも近い岸」なのでしょうか?
以下のように考えてみると、少なくともそうではないことがわかります。
半径v上の点を中心とする、岸に内接する円を描いてみましょう。
鬼が回ってくる方向に少し進んだ先のほうが、若干有利な点であることが、
「ボートの移動量の増分」と「鬼の移動量の増分」の比を考えることでわかるでしょう。
同様に、
円内のある点から、
「円周上の点Aに向かうより、Aよりもう少し先に進んだ点Bに進んだ方が有利になる」
のがどういう場合かを考えると、
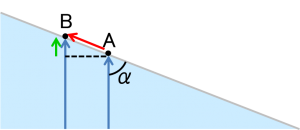
以下の図のように、
接線とのなす角αに対し、
cosα<v
である場合とわかります。
図の、
(赤い矢印の長さ):(緑の矢印の長さ)=1:v
となるαが境目となるわけです。
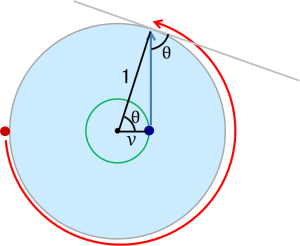
これを踏まえた上で以下の図を見ると、
半径vの円の接線方向に向かうのが最善
ということがわかります。
図で、
θは、v=cosθ となる値です。
緑の円の接線方向に向かう青の矢印と、
到達点における接線とのなす角がちょうどθとなります。
この図で、
鬼に捕まるまでに岸に到達するための不等式を考えるとこのようになります。
v=cosθ なので、この式をθの式で書くとこうなります。
これがイコールになるθは
1.35181…
このとき、
v=0.21723…
1/v=4.6033…
以上より、4.6倍くらいまでなら逃げ切れることがわかりました。
池が円以外の形の場合
池の形が円以外だと、
同じようにはいきません。
そもそも、一般的な図形を考えた場合、
「中心」という点すら自明ではないので、
「同じやり方」を考えるだけでも難しくなります。
図形が凸でないとすると、
鬼が周上を必ず移動するのか、ショートカットできるか、
というルールでも答えは変わるだろうし、
池が有界な領域であったとしても、
周の長さが定義できない場合もあったりしてかなり厄介なことになります。
円の場合が最も「鬼にとって有利」な気はするのですが、
どうやったら証明できるでしょうか?
難しそうなので、池の形が正方形の場合を考えたいと思います。
正方形になるだけで、円の場合よりかなり複雑になります。
長くなったので、正方形の場合は別の投稿とします。
→池の形が正方形の場合

[…] 前回の投稿で、池の形が円の場合について考えました。 […]
[…] 前回と前々回紹介した問題についての続きです。 […]