Taro is here!

前回の投稿で、池の形が円の場合について考えました。

今回は、池の形が正方形だった場合です。
円の場合は4.6倍くらいまででしたが、
正方形の場合は少なくとも5.7倍くらいまでなら逃げ切れます。

以下、
正方形の辺の長さを2、
ボートの速さをv、
鬼の速さを1とします。

とりあえず、単純な方法を考えます。
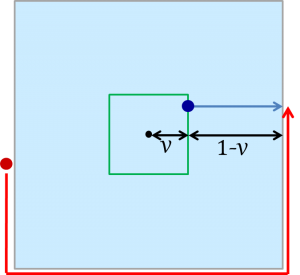
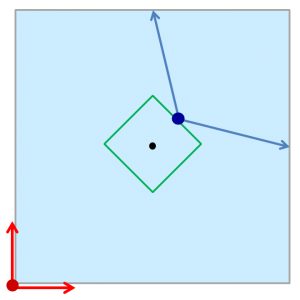
図のような、池のv倍の大きさの緑の正方形の辺上をボートで一周するのと、
鬼が池の周りを1周するのが同じ時間です。
緑の四角形の少し内側を移動すれば、
鬼と遠い位置に来ることができます。

図のように、最も近い辺に垂直に向かう場合に、
ボートが青の矢印を進むのにかかる時間と、
鬼が半周するのにかかる時間が同じになる条件を等式で表すと以下のようになります。

これを解くと、v=0.2 となります。

つまり、鬼の速さがボートの速さの5倍ということなので、
この時点で円の場合の4.6倍を上回っていますね。

ただ、まだまだ最適化の余地があります。

まずは、円の場合と同様に、
鬼が時計回りに向かってくるか反時計回りに回ってくるかで、
向かう先を変えることを考えます。
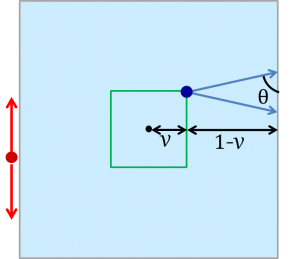
円の場合に考察した通り、
青の矢印と辺とのなす角θが、v=cosθ となる点に向かうのが最善です。

この場合にボートが青の矢印を進むのにかかる時間と、
鬼が半周するのにかかる時間が同じになる条件を等式で表すと以下のようになります。

これを解くと、
v=0.196…
1/v=5.079…

ほんの少しだけ変わりました。

ですが、まだ最善ではありません。

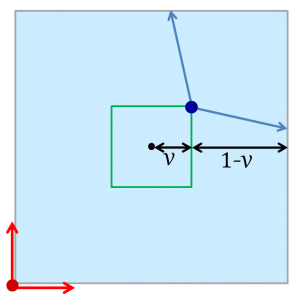
この図のように、緑の四角形の角からは、
鬼の走り出す方向によって、向かう辺を変えてしまった方がよいことは、
想像できるでしょう。

「鬼が途中で方向転換しても大丈夫か？」
というのが問題になりますが、
ちょっと考えるとこれも大丈夫なことがわかります。
（鬼が反対方向に回って来ることを考えた場合に逃げ切れるような鬼の位置の限界点が、鬼の移動速度よりもゆっくりと進むことを示せばよいです）

さて、これを踏まえた上で、ボートは最初にどんな図形の上を回るべきでしょうか？

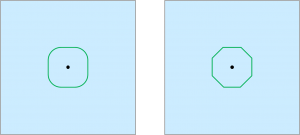
角が取れた形になりそうですが、どうなるか？
と考えると、このような形になることが想像できますが、
検証すると、右のような形になることがわかります。

ただし、右のような形になるのは鬼が十分速い場合で、
鬼の速さがボートの5倍程度の場合は、
8角形ではなく以下のような4角形になります。

ということで、
この緑の正方形を1周するのにかかる時間が、
鬼が1周するのにかかる時間より短ければよいことになります。

しかし、まださらに最適化の余地がありそうです。
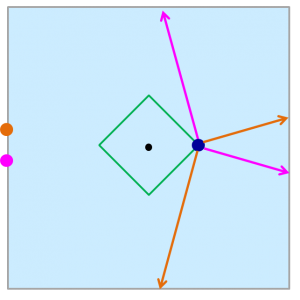
以下の図を見てください。

鬼がピンクの点の位置にいるときは、
鬼の移動する方向を見計らって、ピンクの矢印のどちらかに向かって進めばよいです。
鬼がオレンジの点の位置に角の点から、オレンジの矢印のどちらかに向かって進みます。

ということは、オレンジとピンクの間に鬼がいるときは、余裕があることがわかります。

ということは、もっと最適な逃げ方があるはず！
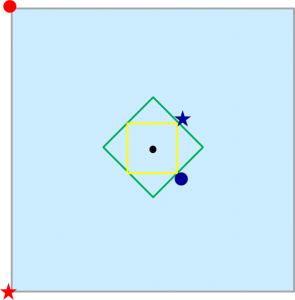
と思って考えるわけですが、そこで、以下の図のように、
緑の四角形の内側に描いた黄色い四角形の上を移動することを考えます。

黄色の辺上からは、鬼がどの位置にいたとしても、
周上の点に向かって一直線に逃げ切ることはできませんが、
ちょうど頂点の位置からは、
図の通り、青の星の位置にいるときに鬼が赤の星の位置にいれば逃げ切れ、
青の丸の位置にいるときは鬼が赤の星の位置にいるときに逃げ切れます。

黄色の一辺をボートが通るのにかかる時間が、
鬼が一辺を移動するのにかかる時間より早ければ、
ボートが星と丸の間にいて、鬼も星と丸の間にいるような位置関係に、
鬼を追い込むことができます。

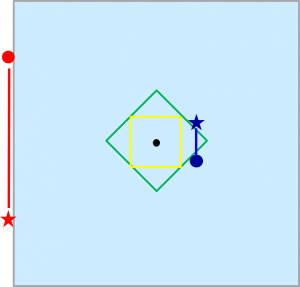
その後、じりじりと外側に向かって鬼を追い込んでいけばよいのです。

この図のように、外側に向かいつつ、
緑の辺上に来る際に鬼がちょうどいい位置に来たら逃げ切れるように、
鬼を追い込んでいけば、
最終的には逃げ切ることができます。

というわけで、
この黄色の四角形の一辺をボートが通るのにかかる時間が、
鬼が一辺を移動するのにかかる時間と同じになる場合を計算すると、
鬼の速さが5.9…倍と出ます。

ただ、これが実際にはうまくいきません。
鬼の速さが5.9倍になってしまうと、
緑の四角形ではなく、先の図で上げたような緑の8角形になってしまいます。
この場合、今の方法ではうまくいきません。

8角形ではなく4角形になるぎりぎりの値を求めると、
鬼の速さは5.78…倍となります。

一般的な場合はどうか

最後は計算式を省略しましたが、
このように、池の形が正方形に変わったことで、
4.6倍から5.7倍に大きく増えることが分かりました。

また、正方形の場合については、
上記の説明ではこれが本当に最適な逃げ方であることまでは示せていません。
なので、実はもっと良い逃げ方があるかもしれません。

正方形になっただけでこれほど複雑度が上がったので、
一般的な図形を考えるのは大変そうです。

せめて、
「凸な多角形を与えると限界の速さを計算するプログラム」
を書いてみたいところですが、
どうやったらできるでしょうか？