「植物は、まっすぐ伸びる茎から、137.5度ずつずらしながら葉っぱを順番に出していくことで、前の葉っぱを隠さず、太陽の光をより多く受けられるようになっているらしい。137.5度という角度が重要。この角度で、松ぼっくりの形も説明できる。」
ということを、前回までの投稿で紹介しました。
この話を踏まえて考えると、色々な疑問が湧いてきますよね。
- 137.5°という角度は何を最適化する値なのか?他の角度ではだめなのか?
- 植物は本当にこの角度に従って成長しているのか?
- 植物の持つ他の角度にも法則はあるのか?例えば、葉の葉脈の角度や、シダ植物の葉っぱの角度など。
- 植物以外にもこの角度は現れるか?動物、地層、宇宙など。
- この問題を3次元以上に拡張するとどうなるか?例えば、球面上に一定のルールで点を順番に配置していくときに、点が均等にばらける条件は?
- 「一定の角度ずつずらす」という制約をなくして、最適な葉っぱの配置を考えるとどうなるか?
1は、前回までの投稿の通り、他にも良さそうな角度はあります。
2は、確かに法則に従っていると思われる植物が多く見つかりますがそうなっていないものも多いです。どうなんでしょうね。
3も気になります。
4は、角度はわかりませんが、黄金比が色々なところに現れるという話は聞きますね。
5は難しそう。
と、このように疑問は尽きないのですが、今回は、6について考えてみましょう。
できるだけ均等に葉を並べる
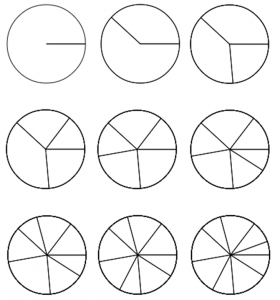
137.5°ずつずらして中心から線を出した図です。
2, 3, 5, 8, 13, 21,… 本のときに、比較的バランスのいい形になるのですが、その間の本数の時は若干いまいちになります。
前回見た「カバー率」を用いると、このことが数値的に測れます。
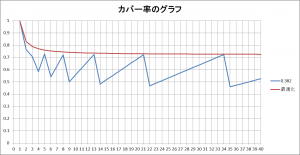
グラフはこのようになります。
青い線が、137.5°ずつ離した場合のカバー率です。
赤い線が、後述の配置方法で線を引いた時のグラフになります。
このように、「一定の角度ずつ離す」という制約をなくせば、何本引いた時も「比較的バランスのいい形」にできるわけです。
ところで、カバー率は、前回は
「隣とぶつからない扇形を並べたときに全体を覆う割合」
と定義しましたが、
「n本の線が出ている状態で、最も近い2本の成す角が、1周の 1/n の何倍か」
と言い表すこともできます。
前回は、植物が「光をできるだけ多く受けられるように」という観点でそう定義したのですが、こう言い換えると、単純に、「2辺をできるだけ離す」と言っているにすぎません。
また、これと逆に、
「n本の線が出ている状態で、隣り合う2辺の最も離れたものの成す角が、1周の 1/n の何倍か」
というのも定義できます。
これは、「できるだけ隙間の空きすぎた部分ができないように」という観点の定式化です。先ほどの赤い線で示したグラフになる配置は、この観点でも良い配置となります。
バランスよく1本ずつ追加していく配置
長い前置きとなりましたが、赤い線のグラフになる配置がどんなものか、見てみましょう。
※表示されない場合はこちらをこちらしてください。
ポイントは、常に、
- 最も離れた角の間に新しい線を引く
- 新しい線によって分けられた2つの角度は、最小と最小から2番目の大きさになる
という状態を保っていることです。
分け方の詳細
1周を1としたときに、以下のように分けています。
1
↓
,
↓
,
,
↓
,
,
,
↓
,
,
,
,
後はこの繰り返しです。
確かに、一番大きいものが、小さい方から1番目と2番目になるように分けられています。うまくできていますね。
何かに応用できないだろうか?
前回のアニメーションで、この順番で葉っぱを出すようにしてみたりもしましたが、全然きれいな形にはなりませんでした。結局、枚数が増えると、1つ前の葉っぱとあまりに近くに次の葉っぱが出てくるので、いまいちなんですよね。
この順番にピザを切ったらどうか?
とも考えたのですが、そうしたいシチュエーションが想像できませんでした・・・。
円形のものには限らないので、羊羹でもいいのですが、やっぱりどこで使えるのかわかりません。
ということで、無理やり応用を考えました。
こんな問題を考えます。
「円形の島の王国があります。
大航海時代が始まり、防衛の必要性を感じた王様は、見張り台と砲台を島の周囲に建設するよう命じました。
しかし、いっぺんに何個も作ることはできないので、造るのは1つずつです。
また、建設には2~3ヶ月かかる上に、来期の予算が本当に下りるかどうかはわかりません。
なので、最終的に4つ作ったところでストップするかもしれないし、10個になるかもしれません。
最初から10個作ると決まっていれば、島の周囲を10等分するように配置するのですが、決まっていないのでそうはいきません。
何個作ったところで建設が終わっても、警備の手薄な場所や砲台が固まって配置された場所ができないようにするには、島の周囲のどの場所に、どのような順番で造っていくのがいいでしょうか?」
普通に考えると、1つ作ったら2つ目はその正反対の側に造りたくなります。
そうしたら3つ目と4つ目は、そのちょうど間に。
こうすると、4つまでで例えば東西南北に1つずつできるわけです。
予算が下りたのでもう1つ作るとなれば、次は北東の方向でしょうか。
ただ、ここでもし次の建設ができなくなってしまったら、
「こんなことなら正五角形になるような位置に造っておけばよかった」
となるわけです。
また、
「敵は最も手薄な場所を狙ってくる」
としたら、
5つ作るのも6つ作るのも7つ作るのも警備の手薄さで言ったら変わりません。
4つ作ったら、もう後4つ作らないと意味がないのです。
こう考えると、1つ追加したら追加したなりの効果が常にあるという意味で、先ほどのアニメーションで示した方向に順番に置いていくのがいいのではないでしょうか。
もうちょっと役立つ応用はないですかね。