黄金角について説明した前回の続きです。
バランスの良い配置を定式化してみよう
角度を一つ決めると、中心からn本の線を引いた時の配置が各nに対して定まります。
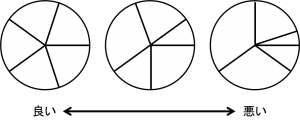
例えば5本の線を引いたときを考えます。
配置の良い・悪い
正五角形を作る、一番左の形が最もよく、間が狭い場所ができる右側の方が悪い形、と考えたいところです。
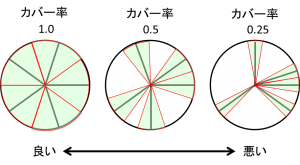
そこで、各線を中心とする葉っぱを、互いに重ならない広さの幅にして並べたときに、どれくらいの面積をカバーするかで定式化してやることにします。
具体的には、以下のように、最も近い線分の成す角度の扇形を並べてやった時に、円の面積の何割をカバーするかで、「カバー率」を定義します。
カバー率の説明
カバー率を、で表すことにしましょう。θを一つ定めるごとに、nの数列が一つ定まることになります。
黄金角のカバー率を見てみよう
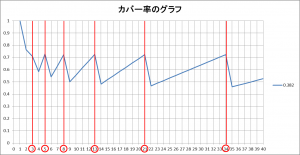
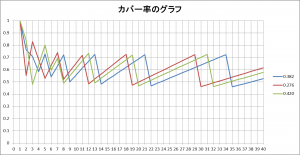
θが黄金角 137.5° のときのカバー率をグラフ化してみました。
黄金角のカバー率のグラフ
ちょうど、フィボナッチ数列の数のときに、カバー率が大きくなっています。
ですが、このグラフで注目したいのは、むしろカバー率が下がった時です。カバー率が下がった時も、0に近づくことはありません。色々計算した結果、カバー率はを下回らないことがわかりました。
このグラフは、このままnを1000, 2000と増やしていっても同じ動きをして、と
の間を行ったり来たりします。（
は黄金比）
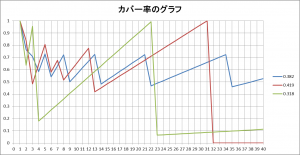
悪い角度のときのグラフと比較してみましょう。
カバー率の比較
赤い線は、角度が一周の 13/31 のときです。n=31 のときに1になりますが、nが31を超えたらカバー率は0です。このように、有理数はいつか0になるのでダメです。
緑の線は、角度が一周の 1/π のときです。これは無理数ですが、黄金角のときと違い、0に近い値まで落ち込んでしまうことがあります。
黄金角以外は全部ダメな角度なの？
このように定義した、「カバー率」の観点でも、黄金角は優れた性質を持つ特別な角度だということが確認できました。
ところが、です。
黄金角以外にも、よい性質を持つ角度はあるのです。
こちらのグラフをご覧ください。
カバー率の良い角度のグラフ化
黄金角は、1周のです。
赤い線の角度は、1周のです。
緑の線の角度は、1周のです。
どれも、 を下回ることがありません。これらは、黄金角と同じくらい良い角度と言えるでしょう。実際、前回の投稿で紹介したアニメーションでこれらの角度を入れると、きれいな形を形成します。
黄金角は無数にあった！！
黄金角は、137.5度のことなので、その他の「良い角度」を準黄金角と呼ぶことにしましょう。
準黄金角を、以下の性質を持つ角度とします。
「あるNが存在して、N以上の任意のnに対して、 が成り立つ」
要するに、最初の数枚はバランスが悪かったとしても、葉っぱの枚数が多くなれば配置がバランス良くなる角度、ということです。上記のグラフに示したのは、準黄金角の中でも特によい性質を持つもので、この条件が全てのnに対して成り立つものです。
色々検証した結果、準黄金角は、以下の形で表せるようです。（必要十分条件であることが厳密に証明できたわけではありませんが、もしかしたら良く知られた事実なのかもしれません。）
「準黄金角は、1周の倍の角度として表せる。ただし、a, m, k は整数であり、かつ、aは
の約数」
mとkは任意なので、適当に選ぶことができます。kを決めると、aはkの約数なので、いくつかの候補に絞られます。
mとkを動かすと、色々な角度に変えられます。その結果、準黄金角は、0°～360°までの間にびっしりと存在することになりそうです。
どんなに狭い区間をとってもその間に有理数が無数にあるのにも関わらず、実数の「ほとんど全て」が無理数であるのと同じです。準黄金角も、ごくごく限定された条件を満たす角度であるにも関わらず、いくらでも存在するのです。
もちろん、準黄金角の条件の「あるNが存在して・・・」のNが大きすぎれば、実質的には「悪い角度」となるのですが。
植物の性質を知るのに役立つかもしれない？
植物によっては、「黄金角になっていないじゃないか！！」と言いたくなるものはたくさんありそうです。
例えば、前回の投稿で示したアロエがそうです。あんなにくっきり5角形の模様が見えるのは、どうも黄金角っぽくありません。
ですが、0.2に近い準黄金角を選べば、中心は5角形っぽいけれど、外側に広がるとバランスのよい感じになります。
以下の図は、前回の投稿のアニメーションの「良い角度1」の角度を「アロエ」の角度にして色を変えたものです。
アロエの葉っぱを増やした場合
ご覧の通り、中心付近は5本のらせんがくっきりと見られますが、外側は均一な感じになっています。
この、準黄金角の考え方を使えば、黄金角で説明できない植物のパターンを、「例外」で片付けずに説明できる場合もあるのではないでしょうか。
アロエが本当にこの角度で葉を出しながら成長しているかどうかはわかりませんけどね。