※解説動画を作りました（YouTube版）（ニコニコ動画版）
パラメータを色々変えることで、植物に現れる幾何学的なパターンを再現できるアニメーションを作成しました。パラメータを直接変えることもできますが、松ぼっくりの裏側やひまわりの中心など、いくつかのプリセットも用意したので、まずはそちらをご覧ください。
最も重要なのは角度です。「ちょうどいい角度」と、「悪い角度」の違いが、視覚的にわかるように、良い角度と悪い角度の例も用意しています。
アニメーションの原理は単純です。中心から葉っぱが、前の葉っぱから一定の角度ずつずらして生えてくるのを繰り返します。葉っぱは楕円です。面積が時刻に比例するように成長します。
単純な仕組みではありますが、楕円の縦横比や色を変えると、松ぼっくりの裏側やひまわりの中心部分っぽい感じになります。面白いですね！
このように、一定の角度ずつずらして葉っぱや花びら、種子が配置されることは、植物に関する性質としてよく知られているもので、解説しているサイトも多くあります。
特徴的なのは、このときにずらす「一定の角度」が、いわゆる黄金比と関係していることと、フィボナッチ数列がパターンの中に現れることです。
黄金比とは、
の表す比率のことで、まあその、いい感じの比率らしいです。
フィボナッチ数列は、
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
と続く数列で、前の2つの値の和が次の値になっています。
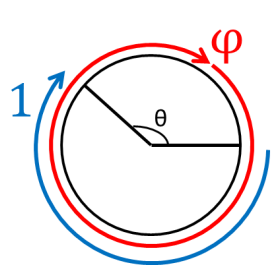
上記のアニメーションで、葉っぱ、松ぼっくりの裏側、ひまわりの中心部分、として用いた「ちょうどいい角度」が、黄金角と呼ばれるもので、以下の図のように1周を黄金比に分けたものです。大体 137.5度です。
黄金角
この角度について解説しているサイトはいくつかあり、その中では、松ぼっくりの模様が描くらせん模様の数が、フィボナッチ数列になっていると説明されています。上記のアニメーションで描かれる図形も、まさにその性質を満たしています。
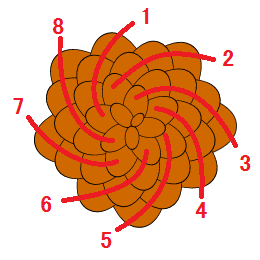
実際、途中で止めると以下のように8本のらせんが見られます。
松ぼっくりの裏側1
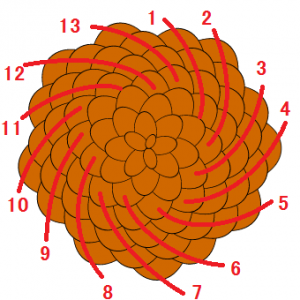
そして、さらに大きくなると、13本のらせんが見られます。
松ぼっくりの裏側2
面白いですね！
フィボナッチ数列が松ぼっくりの模様に現れると言うと不思議ですが、「ちょうど良い角度」ずつ離してうろこを生やして行くと、勝手にフィボナッチ数列が現れるというわけです。
でもちょっと待ってください！！
という話を聞いても、いまいち納得できなかったのは私だけでしょうか？
黄金角というのが「ちょうどいい角度」だというのはわかりました。ですが、「ちょうどいい角度」は本当にそれだけなのでしょうか？もっといい角度はないのでしょうか？
アニメーションの「良い角度1」は、黄金角で松ぼっくりの模様をさらに大きく広げたものです。
黄金角で松ぼっくりの模様を広げ続けたもの
「悪い角度2」です。これは確かにいまいちな感じがします。
悪い角度の例
ですが、「良い角度2」は、黄金角ではないのですが、これもバランスよく広がっています。
黄金角ではない角度
黄金角ではないので、以下のようにらせんの数を数えると、フィボナッチ数になっていません。
黄金角ではない角度のらせんの数
このように、黄金角ではない角度にも「ちょうどいい角度」はあるのです。
実際、植物を見てみても、どう考えても黄金角ではない角度でパターンをつくっているものがあります。
アロエも幾何学模様を作ることで知られており、画像検索すると色々出てきます。
アロエの画像検索
ここまでくっきり5角形を作っているということは、1周の0.2倍か0.4倍に近い角度だけ離れているのでしょう。
バランスの良い配置を定式化してみよう
バランスの良い配置とは何かを定式化して、どんな角度のときにそれが最適となるかを検証する必要がありそうです。
長くなってきたので、これは別の投稿としたいと思います。
→続き
[…] 黄金角について説明した前回の続きです。 […]