Taro is here!

前回の投稿の内容が、読んだ人が同じことをやるには説明が不足していたように思うので、補足します。

ニコニコ動画: 【トランプ】パーフェクトシャッフルの解説とその応用
YouTube: 【トランプ】パーフェクトシャッフルの解説とその応用

こちらの動画で説明したことの一つが、

「52枚のカードを8回パーフェクトシャッフルすると元に戻る」

「N枚のカードがn回のパーフェクトシャッフルで元に戻るための必要十分条件は、 が N-1 で割り切れること」

ということでした。

もう一つは、カードをいくつかの山に配り分けてから適切な順番に重ねるシャッフルについてです。

ここで、N枚のカードをk個の山に分けるシャッフルを k-split shuffle と呼ぶことにしましょう。

具体的には、以下のように行うシャッフルのことを指します。

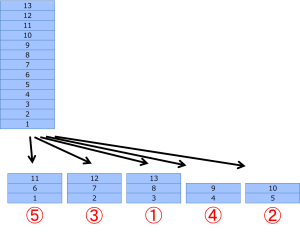
これは13枚のカードを5つの山に分ける例です。
図のように左から右に並べて全て配り終えたら、一番上と一番下のカードが変わらないように重ねて行きます。この例では、①が一番上で、そこから右に向かって一つ置きに、②、③、④、⑤の順にカードを取っていきます。

Nがkで割り切れるときは、右から順に取っていけばいいのですが、そうでないときは、この例のように、一番上と一番下のカードが変わらないように、何個か飛ばして取っていくことになります。この取り方を間違えると以下の法則も成り立たなくなるので、注意してください。
なお、このように何個か飛ばしてすべての山を重ねられるのは、N-1 と k が互いに素（1以外の共通の約数を持たない）であることが必要です。ですので、k-split shuffle は、N-1 と k が互いに素な時しか定義できません。

そして、この k-split shuffle については以下が成り立ちます。

「N枚のカードがn回の k-split shuffle で元の並び順に戻るための必要十分条件は、 が N-1 で割り切れること」

例えば、

なので、ジョーカーを含めた53枚のカードは、 5-split shuffle 4回で元に戻ります。

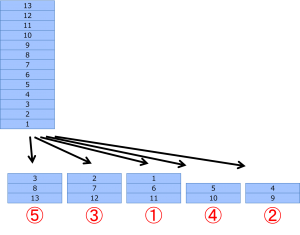
ここで補足です。このシャッフルは、一番下のカードを一番最初に置くことになるので、普通の配り方とは逆の配り方になってしまっています。実用上は、以下の図のように、上からカードを取って順番に置いていくシャッフルをしたいケースの方が多いはずです。

しかし、このような配り方をしても、上下が完全に反転することを除けば、何回で元に戻るかの条件は全く同じです。特に、偶数回このシャッフルを行う場合は、上下の反転を偶数回行った結果並び順が元通りになるので、先ほどの法則が同様に成り立ちます。

よって、53枚のカードを、通常のやり方で5つの山に分けるシャッフルを4回行っても、やはり元の並び順に戻ります。

更なる一般化

もう一つの動画では、7-split shuffle, 5-split shuffle, 3-split shuffle を行って、52枚のカードの並び順を元に戻していました。

ニコニコ動画：【トランプ】混ぜたはずが元に戻った！？の手品とその解説 (6:36)
YouTube: 【トランプ】混ぜたはずが元に戻った！？の手品とその解説

こちらについての説明ですが、まず、以下が成り立ちます。

「N枚のカードに対して、k-split shuffle と m-split shuffle を行った結果の並び順は、km-split shuffle を行った結果と等しい」

このことから特に、

「k-split shuffle を行ってから m-split shuffle をするのと、m-split shuffle を行ってから k-split shuffle をした結果は同じ」

ということも言えます。

そして、これらのシャッフルを組み合わせて元に戻るための条件は以下のように表せます。

「N枚のカードが -split shuffle, -split shuffle, -split shuffle, ・・・ を行った結果元の並び順に戻るための必要十分条件は、 が N-1 で割り切れること」

7×5×3-1=104=52×2

なので、53枚のカードに対して 7-split shuffle, 5-split shuffle, 3-split shuffle を行うと元の並び順に戻ります。

動画中では、最初に配る際に、
「裏向きの山を表に向けながら配る」
ことで、上下の反転を防いでおり、また、
「端にあったスペードのAの前にもう一枚カードがあるつもりでシャッフルする」
ことで、1枚足りないのをカバーしていました。

このように、本来N枚でやるところを、位置の変わらない両端のカードを取り除くことで、N-1枚やN-2枚でやることもできるわけです。シャッフル何回で元に戻るかは計算の結果で完全に決まってしまいますが、このような工夫で多少の自由度を持たせることは可能です。

更なる一般化の結果の考察

N枚のカードをk-split shuffle した結果の並び順は、何通りあるでしょうか？

実はこれは、

「1 以上 N-1 以下の整数で、 N-1 と互いに素なもの」

と、1対1に対応します。

この個数は、オイラーのφ関数(Wikipedia)と呼ばれるのものに他なりません。

数学の群論の言葉で言うと、
「N枚のカードに対する k-split shuffle の全体は可換群を成し、その位数は φ(N-1) である」
と言えます。

また、最初に挙げた、k-split shuffle 何回で元の並び順に戻るかと言う話は、フェルマーの小定理(Wikipedia)と、同じページに説明のあるカーマイケルの定理で具体的に求められることになります。

フェルマーの小定理の一般化・応用の先にはミラー・ラビン素数判定法(Wikipedia)なんかもあるので、ちょっと工夫すれば、k-split shuffle で、手元にあるカードの枚数が素数かどうかを判定できるかもしれませんね！