こちらは、三角関数の、y=sin x のグラフです。
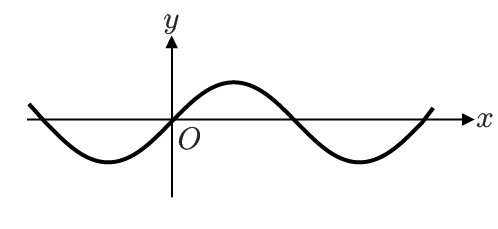
y=sin x
高校の授業で出てくるおなじみのグラフですが、今回のテーマは、
この、サインカーブを折り目にして紙を折ると、どんな形になるか？
です。
「そんなこと考えたこともない」
「そもそも曲線の折り目で折るって何なんだ？」
という方がほとんどではないでしょうか。
ですが、筑波大学の三谷先生の立体折り紙アートが話題になったりしたこともあり、曲線で折る折り紙が、一部でブームになっているのではないか、という気もしています。
ということで、作ってみたのがこちらです。
サインカーブの折り目の箱の展開図
サインカーブで折り目を付けた、展開図です。
これで箱を作ってみると、こうなります。
サインカーブで折った箱(1)
サインカーブで折った箱(2)
サインカーブで折った箱(3)
元の紙があんな形だったのに、線に沿って追っただけで、こんな湾曲した曲面の箱に仕上がるのは、なかなか不思議ではありませんか？
特に、この3枚目の、まっすぐな方向から見たときのシルエットには特徴があります。
カーブが、ちょうど円の一部、半円の曲線になっているのです。
半円の形
完成したものを動画で映したほうが分かりやすいでしょうか。
先ほどの形です。これがあの展開図からできるというのは、ちょっと想像し難いところがあります。
さて、これを応用して、完成したときのシルエットが任意の曲線になるようにできないでしょうか？ pic.twitter.com/lYcE8JKmqS
— Yusuke Ochiai (@taro_x) October 8, 2016
「本当にそんな形になるの！？」
と思った方は、正確でなくてもいいので、紙にサインカーブっぽい曲線を描いて、紙を曲げてみてください。
それだけでも、「なんとなくこういう形になりそうだ」ということは分かるはずです。
この原理をさらに応用できないだろうか？
さて、この、サインカーブを折り目にして折った箱ですが、ちょっと面白いのは、まっすぐな方向から見たシルエットが、円の一部になっていることです。
これを一般化して、
ある与えられた曲線が、完成したときのシルエットになるような折り目を計算することはできないだろうか？
ということを考えてみたいと思います。
