Taro is here!

猫とロボットを重ねるとドラえもんになるものが大変好評だったので、実際にやってみたい人もいるかと思い、別の絵柄ですが、重ねると全く違う絵柄が浮き出るものの販売を始めました。 さて問題です。ロボットの切り絵と猫の切り絵を重ね

京大特色入試に超難問　数学の筆記試験“五輪級” こちらの記事が話題になっていたので、問題のシミュレータを作りました。 ※うまく表示されない場合は、こちらをクリックしてください。 n=2345678910111213141

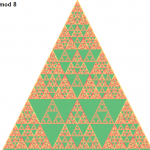
前回の記事で、パスカルの三角形を色分けすると様々な不思議な模様が現れるのを見ました。 今回は、それを応用して平面を埋めつくすパターンを考えてみましょう。 前回のおさらい 前回やっていたことは何かと言うと、パスカルの三角形

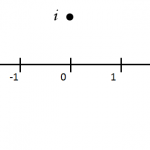
「虚数って何？意味あんの？」と高校生に言われたらどう答えるか では、 この2次方程式は実数解を持たない。でも、「解なし」じゃ困る。どうしても解がほしい と思えるような、2次方程式の例を考えました。 この話は、つい先日話題

高校数学で複素数を習った際、 「何これ？何の意味があるの？」 という疑問を持った人は多いのではないでしょうか。 それまでは、 「2次方程式は、解を持つ場合と持たない場合がある」 という話だったのに、それを無理矢理 「2乗

黄金角について説明した前回の続きです。 バランスの良い配置を定式化してみよう 角度を一つ決めると、中心からn本の線を引いた時の配置が各nに対して定まります。 例えば5本の線を引いたときを考えます。 正五角形を作る、一番左

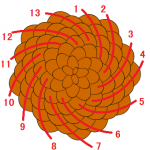
※解説動画を作りました（YouTube版）（ニコニコ動画版） パラメータを色々変えることで、植物に現れる幾何学的なパターンを再現できるアニメーションを作成しました。パラメータを直接変えることもできますが、松ぼっくりの裏側

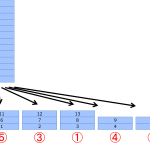
前回の投稿の内容が、読んだ人が同じことをやるには説明が不足していたように思うので、補足します。 ニコニコ動画: 【トランプ】パーフェクトシャッフルの解説とその応用 YouTube: 【トランプ】パーフェクトシャッフルの解

わかっててやっても不思議な、混ぜたのに混ざらないトランプの性質を動画で解説しました。 ニコニコ動画： 【トランプ】混ぜたはずが元に戻った！？の手品とその解説 (6:36) YouTube： 最初は、トランプ一組のうちの半

前回作ったものが分かりづら過ぎたので、途中経過が見えるようにしました。 Previous version 同じ四角形を2回クリック（タップ）すると、その場所に応じて絵が変化します。Goalの形にできたら終了です。 ※正し

こちらのゲームについての説明です。 変形のルールについて 青いテーブルのセルをクリックすると数字が変化しますが、そのルールは以下の通りです。 テーブル内の数字は、0から4までの整数値のみを取る。足し算や掛け算は、通常の整

This is an explanation about this game. Rule of transformation The numbers will be changed according to the fo

前回の改良版です。 鬼がどこまで移動できるのか、とても暗算では計算できないので、ガイドを表示するようにしました。 ※表示されない場合はこちらをクリックしてください。 ※ガイドが表示されるのは、PCでマウスオーバーした場合

前回と前々回紹介した問題についての続きです。 Aさんは円形の池の真ん中でボートに乗っています。 岸には、Aさんを捕まえようと待ち構えている鬼がいます。 鬼はボートの4倍の速さで池の周りを走れます。 Aさんは鬼に捕まること

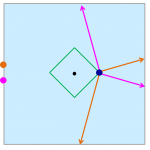
前回の投稿で、池の形が円の場合について考えました。 今回は、池の形が正方形だった場合です。 円の場合は4.6倍くらいまででしたが、 正方形の場合は少なくとも5.7倍くらいまでなら逃げ切れます。 以下、 正方形の辺の長さを